Il y a quelques temps, j'avais promis de reparler du graveur Escher, en évoquant la réalisation, par un designer allemand, de sa fontaine infinie. Chose promise, chose due, voici donc un petit article sur Maurits Cornelis Escher, artiste réaliste, méticuleux, obsédé par la géométrie et les répétitions infinies.
Une brève histoire d'estampe
 Escher naît en 1898 aux Pays-Bas. Son talent est découvert et encouragé très tôt; il s'oriente rapidement vers les arts graphiques, notamment vers la gravure (ce qui explique la dominance des œuvres en noir et blanc). En 1922, ses études terminées, il voyage dans le sud de l'Europe, où il passe son temps à recopier et à dessiner ce qui lui tombe sous les yeux. Son imagination restera marquée par les caractéristiques architecturales des monuments visités: voûtes, escaliers, mosaïques, pavages réguliers etc. Comme beaucoup d'artistes, Escher vit pauvrement. Il quitte l'Italie Mussolinienne pour se rapprocher de la Hollande et s'installe tardivement en Belgique, en 1937. Cette date marque un tournant dans son travail, qui incorpore désormais des éléments fantaisistes.
Escher naît en 1898 aux Pays-Bas. Son talent est découvert et encouragé très tôt; il s'oriente rapidement vers les arts graphiques, notamment vers la gravure (ce qui explique la dominance des œuvres en noir et blanc). En 1922, ses études terminées, il voyage dans le sud de l'Europe, où il passe son temps à recopier et à dessiner ce qui lui tombe sous les yeux. Son imagination restera marquée par les caractéristiques architecturales des monuments visités: voûtes, escaliers, mosaïques, pavages réguliers etc. Comme beaucoup d'artistes, Escher vit pauvrement. Il quitte l'Italie Mussolinienne pour se rapprocher de la Hollande et s'installe tardivement en Belgique, en 1937. Cette date marque un tournant dans son travail, qui incorpore désormais des éléments fantaisistes.Son style est précis, détaillé, il n'y a pratiquement pas de place pour le flou. Ses techniques de travail limitent souvent l'usage de la couleur mais sa maîtrise du dessin, de la perspective, des contrastes et des formes est impressionnante. Escher est un analyste qui décrit des structures, se les approprie et les transforme. Il est fasciné par la géométrique, la symétrie, l'ordre, la perspective et les motifs répétés. Il passe énormément de temps en études préliminaires et en travaux préparatoires. Pour autant, même si les titres de gravures sont d'un prosaïsme rebutant, ses dessins complexes ne sont pas ennuyeux, au contraire; ils sont narratifs et perturbants. Son œuvre n'a pas d'équivalent en Europe mais trouve un écho intéressant dans les constructions géométriques arabes (dont il verra des exemples en Espagne) et indiennes. Ses contemporains préfèrent un art moins cérébral, plus chaotique.
 |
| Saint François |
Durant sa vie d'artiste, Escher montre un grand intérêt pour certains aspects des sciences. Il est sensible à l'esthétique et à la pureté des modèles mathématiques ou physiques par exemple. Il montre également un grand intérêt pour l'astronomie et la théorie de l'évolution. Les scientifiques sont également nombreux à se servir de ses dessins pour illustrer certaines notions, ils en apprécient la clarté et l'élégance des symétries ; ses œuvres les plus célèbres sont d'ailleurs devenues des images incontournables en cristallographie. Cette réciprocité donnera lieu à des échanges entre l'artiste et certains scientifiques. Escher aime les mathématiques mais son attirance pour cette
discipline est avant tout visuelle. Son travail se nourrit de notions
précises que l'on retrouve en effet en géométrie, en
topologie ou en cristallographie, mais Escher s'attache à une
description purement graphique des structures et ne s’embarrasse pas du
formalisme mathématique associé. Il est toutefois frappant de voir avec
quelle exactitude certains de ces dessins reflètent des concepts
scientifiques précis. C'est tout cela que je me propose de vous faire (re)découvrir aujourd'hui. Je ne suis pas historien de l'Art, aussi je m'arrête ici pour la biographie. Pour en savoir plus, vous pouvez consulter le site officiel.
La transformation de la réalité: la projection et la structure
 |
| Polyèdres |
Escher travaille également sur d'autres transformations, parfois purement fantaisistes, comme dans l'exemple ci-dessous, où l'on peut voir le canevas préparatoire utilisé pour déformer le centre de l'image.
Son travail sur la réflexion et la déformation est remarquable. On peut aussi voir, à gauche, un exemple de déformation ondulatoire, qui forme des entrelacs dans la réflexion de la flaque d'eau. Le résultat est quasiment parfait. Il faut pourtant effectuer plusieurs transformations complexes pour y parvenir : projeter dans un premier temps des cercles concentriques sur une surface plane vue en perspective puis appliquer une déformation circulaire à l'image de base. Cette habilité à manipuler les transformations lui vaudra la sympathie des mathématiciens, notamment en théorie des groupes, pour qui les notions de symétrie, d'image et de transformation sont fondamentales.
Sur le dessin de droite, Exposition d'Estampes, Escher a laissé un disque vide au centre. Pourquoi ? Cette "incomplétude" était elle préméditée? Il est vraisemblable que la grille de transformation ait été trop difficile à utiliser sur cette petite partie centrale, même pour Escher. Des chercheurs, aidés par l'artiste néerlandaise Jacqueline Hofstra, ont analysé les transformations complexes de la grille et imaginé la partie manquante. Le résultat, visible en vidéo ci-dessous, est une mise en abîme où le dessin se tord dans un tourbillon infini :
Escher le cristallographe
La spécificité des cristaux (comme le sel, le sucre, le diamant, et de façon générale, tous les minéraux) est de présenter une structure périodique parfaitement ordonnée à l'échelle atomique. Le sel de table par exemple, le chlorure de sodium, est constitué de milliards de "petits cubes" qui ressemblent à ceci (les boules vertes représentent les atomes de chlore et les boules bleues, les atomes de sodium) :
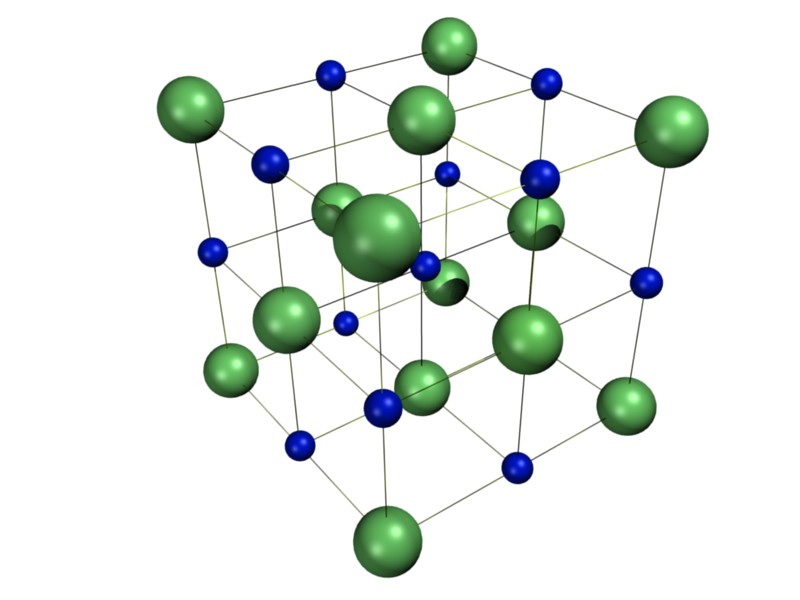 |
| Structure cristalline du sel de table |
 |
| Une structure tridimensionnelle d'Escher |
Escher, séduit par cette simplicité symétrique, s'empare du concept et invente des motifs particulièrement sophistiqués. Dans l'exemple ci-dessous, j'ai tracé les lignes de symétrie. Le losange rouge montre le motif qui est répété (on peut choisir ce que l'on veut comme motif, pourvu que l'on puisse reconstituer l'intégralité du dessin en le répétant).
La description formelle des structures cristallographiques fait aussi
intervenir la théorie des groupes. Pour décrire une structure, on donne la forme du réseau cristallin de base -un cube par exemple- et les opérations de symétrie qui laissent le système cristallin invariant, c'est à dire inchangé. Autrement dit, on peut partir d'un motif élémentaire et
reconstituer l'ensemble du réseau de base par des opérations de
transformation. Cela semble un peu compliqué, alors voici un petit
exemple de transformations possibles en 2 dimensions, avec une pomme et
une banane comme motif élémentaire et un réseau de base comportant 8 pommes et 8 bananes. En juxtaposant des carrées remplis de la même façon, on forme un cristal en 2 dimensions.
Tout en s’intéressant à la cristallographie, Escher explore un autre domaine des mathématiques lié à la question suivante : pour une forme donnée, quel est le meilleur arrangement sur une surface plane, celui qui permet le moins de pertes ? Dans les dessins d'Escher, les pertes sont nulles, car il peut choisir de déformer les motifs à volonté. Cette question a des applications pratiques, comme lorsque l'on veut découper un maximum de pièces en aluminium sur une plaque la plus petite possible. Voici d'autres exemples de pavage astucieux imaginés par Escher :
Il est intéressant de noter que Roger Penrose, dont nous verrons plus loin qu'il a été une source d’inspiration pour Escher, publiera en 1970 un article sur des pavages non périodiques qui permettent de remplir le plan. Ces pavages n'avaient à l'époque aucune correspondance dans le monde réel. En 1984, ils seront utilisés pour décrire la structure des quasi-cristaux récemment découverts.
L'élégante symétrie
Le principe de symétrie est omniprésent en physique. La chiralité par exemple, est une notion qui concerne la symétrie "miroir". Si un objet possède une image dans un miroir, avec laquelle il ne se confond pas, on dit qu'il est chiral. Vos mains, par exemple, sont des objets chiraux : la main gauche est bien l'image de la main droite dans un miroir mais il est impossible de les confondre si on les superpose. Une balle de ping-pong par contre, est indiscernable de son image dans miroir : ce n'est pas un objet chiral. La notion de symétrie est aussi reliée à une question fondamentale: pourquoi notre Univers est il constitué de matière, et non d'antimatière ? Les équations de la physique sont pourtant symétriques : chaque particule possède une antiparticule qui a une charge opposée. Comme les équations sont symétriques par rapport au temps aussi, on peut considérer l'antimatière comme de la matière "normale" qui remonte le temps (il va falloir que j'en parle dans un prochain article). Mais pourquoi l'antimatière semble t-elle avoir disparu de notre Univers ? En 1957, le prix Nobel de Physique est attribué, entre autres, à Chen Ning Yang, pour son travail sur la non-conservation de la parité de l'interaction faible. Cette théorie de physique quantique décrit la violation d'un type de symétrie lors de certaines réactions entre particules. Il montre ainsi qu'une expérience réalisée avec de la matière n'est pas l'exact reflet dans un miroir de la même expérience réalisée avec de l'antimatière. Pour illustrer ses propos, il utilise la gravure Cavaliers :
 |
| Cavaliers |
En plaçant un miroir vertical au milieu de l'image, le motif des cavaliers blancs (la matière) devient effectivement celui des cavaliers noirs (l'antimatière) mais il faut rajouter une translation verticale, c'est à dire qu'il faut déplacer le motif obtenu vers le haut ou vers le bas, pour qu'il se superpose à lui même.
Dialogues sur l'infini
 |
| Développement |
Il revient aux motifs après une correspondance avec le mathématicien canadien H.S.M. Coxeter. Ce dernier lui fait découvrir la géométrie hyperbolique inventée par Poincaré. Il s’intéresse alors aux pavages circulaires limites, avec une série de xylogravures (gravures sur bois) remarquables où le motif est répété indéfiniment et de façon décroissante. Ces figures ressemblent aux projections stéréographiques, également utilisées en cristallographie. Plus tard, frustré par les limitations de la feuille plane, Escher revient à la sphère : il réalise des sculptures à motifs en forme de boule. Ainsi, quelque soit la direction suivie à la surface de la sphère, le motif se répète sans arrêt.
 |
| Projection stéréographique du diamant |
 |
| Escher travaillant sur un motif circulaire infini |
 |
| Limites circulaires |
Ces travaux graphiques sont une excellente illustration de certaines notions mathématiques, comme celle de limite par exemple. Le mathématicien D.J.Lewis dira : "De même que les estampes de M.Escher, les plus beaux résultats ont souvent pour conséquence une approximation systématique combinée à quelques sujet ingénieux et approprié". Sa renommée grandit chez les scientifiques et on porte à sa connaissance d'autres objets mathématiques intéressants d'un point de vue topologique, dont le fameux ruban de Möbius : un ruban qui ne comporte qu'une seule face et dont on peut parcourir la totalité de la surface de façon continue. Escher s'en sert pour illustrer une nouvelle fois l'infini : les fourmis parcourent indéfiniment la même face du ruban. Il travaille également sur d'autres objets topologiques apparentés, comme dans Nœuds ou Spirales.
Dans un de ces dessins les plus connus, Reptiles, on retrouve une boucle perpétuelle ainsi que le thème du passage de l'abstrait au vivant (et vice et versa). Escher y montre aussi son intérêt pour la théorie darwinienne en particulier et pour le passage du chaos à l'ordre en général.
 |
| Reptiles |
 |
| Mains |
 |
| Le principe holographique |
Escher, la force créatrice et le pouvoir de l'illusion
 |
| Enroulement |
Un article du mathématicien anglais Roger Penrose sur les objets impossibles et les illusions d'optique (British Journal of Pshychology) fournit à Escher une nouvelle façon de reprendre le thème de l'infini et de truquer la réalité. Il utilisera par exemple l'escalier de Penrose pour créer des scènes surréalistes où les lignes de fuite sont interchangeables :

Une version plus mouvementée :
Si Escher est fasciné par l'absolue perfection des concepts mathématiques, il reste persuadé qu'ils n'ont pas d'équivalents dans le monde réel. Ses représentations sont au mieux une illusion, une réflexion déformée. La sensation vertigineuse que l'on éprouve en regardant ses dessins renvoie à notre propre conception de l'infini. On retrouve cette façon de jouer avec les illusions dans quelques dessins célèbres:
Psychologie de la forme et philosophie
La psychologie de la forme (ou Gestalt theorie) expose les lois fondamentales de la perception. A mi-chemin entre biologie et psychologie, elle décrit la manière dont notre cerveau traite automatiquement une image comme un ensemble structuré (et non comme une simple addition ou juxtaposition d'éléments). Peut être un peu ennuyeuse dans son énoncé, elle est au contraire très amusante dans l'observation. En effet, la plupart des illusions d'optique trouvent une "explication" dans la théorie des formes. Notre cerveau a par exemple l'habitude de s'attacher aux contours et à compléter spontanément les formes incomplètes. Qui plus est, en analysant la totalité d'une image, il équilibre les différents éléments, quitte à les transformer un peu, pour fournir une perception claire et rapide. Cette apparente unité opposée à la somme des éléments dénués de sens est érigée en principe philosophique par certains : "le tout est différent de la somme de ses parties". Notre compréhension du monde dépend donc de ces processus qui permettent de le percevoir dans sa globalité.Loin de ces considérations théoriques, Escher élabore des dessins qui serviront d'illustrations aux lois de la théorie des formes. Les illusions de perspectives présentées précédemment peuvent être analysées comme suit : elles sont perturbantes car notre cerveau, bien qu'il parvienne à détailler les différents éléments (on peut par exemple suivre le chemin du cours d'eau perpétuel), n'est pas en mesure de produire une perception globale cohérente et intelligible. L'illusion du dessin Cube par exemple, un autre objet impossible, est basée sur le fait que notre cerveau interprète individuellement les différentes parties du cube et cherche à en fabriquer une image homogène. Ce phénomène est illustré ci-dessous, avec à gauche, le cube de Necker et à droite, le cube d'Escher.

Si vous regardez le cube de gauche, votre cerveau va automatiquement choisir de considérer la face en bas à gauche comme la face la plus proche de vous, car il préfère "voir" le cube d'en haut. Mais si vous concentrez votre attention sur la face en haut à droite (interprétation 2 ci-dessous), votre cerveau acceptera éventuellement de la considérer comme la face la plus proche, comme si le cube était vu du dessous. Cette distinction est plus facile si on met une des deux faces en évidence (le contour bleu est celui de la face la plus proche) :
Dans les dessins suivants, Escher joue avec les contours et les frontières. Du point de vue de la Gestalt theorie, ces éléments forcent le cerveau à créer une distinction artificielle au niveau des formes, en s'appuyant sur le contraste entre figures noires et blanches.
On remarquera que Prédestination est un des rares dessins à ne pas avoir un titre strictement descriptif ! Escher réalise également la série suivante :
Escher aurait il fait un bon scientifique ? Il me semble que sa curiosité et la façon dont il a méticuleusement exploré les possibilités de ses découvertes successives appellent une réponse positive. J'espère vous avoir donné envie de découvrir son travail plus en détail ! Si vous visitez les Pays-Bas, faites un détour par La Haye (Den Haag) et visitez le Escher Museum plutôt que le TPI.
Pour illustrer cet article, je me suis restreint à un petit nombre de dessins, mais Escher a produit d'autres pièces remarquables. A titre personnel, le dessin que je préfère est celui-ci:
 |
| Neige |
Les dessins les plus célèbres d'Escher ont été maintes fois repris ou parodiés. Cela me fournit l'occasion de conclure, en images toujours, avec quelques références des Simpson, et un gif animé :
Pour en voir ou en savoir plus :
- Sur Escher et ses œuvres: le livre "Le monde de M.C.Escher", J. L Locher la page "officielle", ainsi que celle du musée des beaux arts canadien.
- Sur d'autres parallèles intéressants, le livre "Gödel, Escher, Bach, Les brins d'une guirlande éternelle" de Douglas Hofstadter.
- Sur le remplissage du tableau "Exposition d'estampes", ce site.
- Sur les commentaires du mathématicien Coxeter au sujet des travaux d'Escher, cette vidéo.
- Sur Escher et les maths, cet article (en anglais).
- Sur l'escalier de Penrose, la page wiki.
- Sur les pavages de Penrose, pareil.
- Sur les transformations géométriques dans les dessins d'Escher, cette page.
- Sur le problème des pavages d'Escher, cette page.
- Sur les parodies artistiques des Simpson, ce site.
- Sur les illusions d'optique, ce site.
Si vous aimez les maths, je vous conseille ce blog formidable.
Et si vous aimez le lien entre les sciences et l'art, je vous invite à consulter ces articles!
Allez, un dernier pour la route:
Et si vous aimez le lien entre les sciences et l'art, je vous invite à consulter ces articles!
Allez, un dernier pour la route:


























Excellent article ! Probablement le plus complet, clair et exhaustif que j'ais lu jusqu'à présent à propos d'Escher et des sciences. Ça éclaire notamment sous un angle différent les commentaires qu'il a lui même laissé sur ses oeuvres dans "M.C. Escher - L'oeuvre graphique" dans lequel il s'avoue justement ignorant de toutes ces spéculations de mathématiciens autour de lui.
RépondreSupprimer(Juste une petite faute d'orthographe relevée: "Escher aimait les mathématiques mais son attirance pour cette discipline était avant tout visuelLE.")
Merci beaucoup! Et merci pour la correction, je deviens laxiste, honte sur moi!!!
RépondreSupprimerJe vous recommande aussi d'écouter l'interview passionnant d'Arthur Escher, célèbre géologue (suisse) et fils de Maurits Cornelis. Il raconte entre autre les pénibles débuts de l'artiste. C'est ici http://www.rts.ch/la-1ere/programmes/impatience/3985255-portrait-d-arthur-escher-25-05-2012.html
RépondreSupprimerJ'écoute en mangeant:)
RépondreSupprimerMerci beaucoup pour cet article passionnant! =)
RépondreSupprimerMerci pour votre commentaire :)
RépondreSupprimertres tres bon article
RépondreSupprimertrès instructif
RépondreSupprimerMerci merci :)
RépondreSupprimerJe suis très heureuse d'être tombée sur cette article dans mes recherches ayant un exposé à préparer sur escher et cherchant des explications sur l'utilisation des mathématiques dans ses oeuvres
RépondreSupprimerMerci pour votre commentaire !
RépondreSupprimerWaouh ! Waouh ! Tout d'abord, j'ai un immense respect et fascination envers les oeuvres d'Escher que je découvre grâce à vous, cher Kevin Madjer. Ensuite votre article est superbe et colossal en matière de recherches. Devant avant tout faire des recherches mais lutter contre mon "syndrome Wikipédia"^^je n'ai pas tout cherché, tout du moins pas en profondeur, notamment les liens avec les mathématiques très complexes évoquées. Lorsque j'aurai plus de temps je lirai plus de vos articles; je ne lis pas vraiment de blogs (et je devrais, bien que le temps puisse me manquer) et le vôtre a l'air extrêmement méticuleux et original ! De plus, vous semblez mélanger art et sciences. En tant que future poussière d'étoile de 16 ans désirant devenir mangaka et qui adore apprendre de tout, cela m'a l'air d'être un bon moyen de recoller les morceaux avec les mathématiques (ces deux dernières années, le système scolaire me l'a fait détester et sombrer) et les sciences en général que j'ai pas mal délaissées.
RépondreSupprimerEncore une fois très bon article, avec des liens externes, bref, rien à dire si ce n'est "waouh" ! Dans ces temps de regroupement des activités sur le web en une dizaine ou vingtaine de sites (qui est un bien et un mal), ça me redonne confiance en la créativité des sites web !
exellent article merci beaucoup;fiere d'etre suisse meme si on n'est pas tous géniaux!hihihi
RépondreSupprimerMerci Karim Madjer pour cet article de vulgarisation. Je reviens de La Haye et du musée Escher (que j'ai adoré). Et je cherchais un peu de documentation supplémentaire et accessible pour une non-scientifique (c'est le moins qu'on puisse dire!). Cet Hollandais (Rendons à Jules ce qui est à Jules... ) me semble être assez obsessionnel.
RépondreSupprimerCancre en classe, une fois qu'il a eu trouvé ce qui le motivait (le dessin, la gravue,etc.) il a avalé des mathématiques, des sciences en général et les a portés haut dans sa quête de l'infini.
Merci et bon vent.
Remerciements tardifs, comme d'habitude, pour ce gentil commentaire. J'étais allé à La Haye sans voir le musée :( Mais il me reste quelques décennies pour réparer cette injustice (j'espère )!
RépondreSupprimerTres bien resume!
RépondreSupprimerComme notre monde est plat et vide et aussi dense foisonnant grandiose et impalpable.
Quelle harmonie ds toutes les combinaisons de Echer qui representent la perfection De notre Univers. Seul Le Createur Supreme est leGrand Artiste.